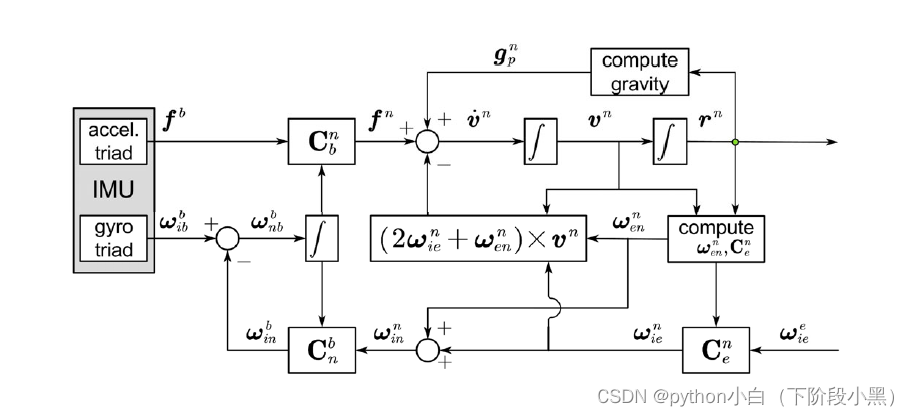
 # 摘要 惯性测量单元(IMU)传感器在数据采集和处理中扮演着关键角色,而滤波算法对于提升IMU数据的质量至关重要。本文首先介绍了IMU传感器及其数据处理的基础知识,随后深入探讨了各种常见滤波算法的理论基础和分类。通过分析卡尔曼滤波器、帕斯瓦尔滤波器和粒子滤波器等算法,我们着重讨论了它们在IMU数据处理中的应用与性能评估。文中还提供了环境噪声对IMU数据影响的分析及消除技术,并详细阐述了滤波算法的实现步骤和滤波结果的优化方法。最后,通过民用和工业领域的应用案例,本文展示了IMU数据滤波算法的实际效果,并预测了滤波技术未来的发展趋势,包括多传感器数据融合和人工智能在滤波中的潜在应用。 # 关键字 IMU传感器;数据处理;滤波算法;卡尔曼滤波器;环境噪声;多传感器融合 参考资源链接:[基于STM32的GPS与IMU数据采集处理项目](https://wenku.csdn.net/doc/88nz0jn9zi?spm=1055.2635.3001.10343) # 1. IMU传感器与数据处理基础 ## 1.1 IMU传感器的工作原理 惯性测量单元(Inertial Measurement Unit,IMU)是现代技术中不可或缺的传感器,它通过组合加速度计、陀螺仪和磁力计,测量和报告一个物体的特定动态参数,例如加速度、角速度和磁场方向。加速度计能够测量线性加速度,而陀螺仪则能够检测角速度,磁力计则能提供磁场方向信息。IMU在没有外部参照的情况下,能够提供物体在空间中的移动信息。 ## 1.2 数据处理的必要性 IMU采集的数据常包含噪声和误差,为了准确获得物体的运动状态,必须对原始数据进行处理。这通常包括消除噪声、校正传感器偏差以及应用各种数据融合技术。数据处理的另一个目的是将来自不同传感器的数据有效整合,以提供更准确的运动估计。这些处理步骤是实现高精度导航和稳定控制的关键。 ## 1.3 数据处理流程简介 数据处理流程通常包括以下几个步骤:数据采集、预处理(如滤波去噪)、数据融合、估计与解算(如姿态估计算法),以及输出最终的运动状态信息。预处理阶段,通常采用低通滤波、中值滤波等简单方法去除高频噪声。数据融合阶段,可能涉及卡尔曼滤波器等高级算法,整合多传感器数据。解算姿态时,可能需要处理三维空间中的旋转和平移,使用四元数和欧拉角等数学工具。最后,输出的运动状态信息可以用于导航、定位、控制系统反馈等。 # 2. 滤波算法的理论基础 ## 2.1 滤波算法概述 ### 2.1.1 滤波算法的目的和重要性 滤波算法是信号处理领域的一项核心技术,其目的是从信号中移除不需要的成分,如噪声和干扰,同时保留有用信息。在IMU数据处理中,滤波算法的重要性尤为凸显,因为传感器数据通常包含了大量随机噪声和确定性误差。滤波算法的正确应用,不仅能提升数据的准确性,还能增强系统对真实运动状态的估计能力,这对于任何依赖IMU数据的系统性能都是至关重要的。 ### 2.1.2 主要滤波算法的分类 滤波算法可以按照不同的标准进行分类。依据模型的线性特性,主要分为线性滤波算法和非线性滤波算法。线性滤波算法中最著名的是卡尔曼滤波器,而非线性滤波算法包括粒子滤波器和扩展卡尔曼滤波器等。另外,根据数据是否事先已知,滤波算法还可以分为递推滤波和非递推滤波。 ## 2.2 常见滤波算法解析 ### 2.2.1 卡尔曼滤波器 卡尔曼滤波器是一种高效的递推滤波器,它通过构建一个线性动态系统的状态模型,利用预测-校正机制来估计系统的最优状态。卡尔曼滤波器在处理时序数据和动态系统时,能够有效滤除噪声,并且实时更新状态估计值。 ```mermaid graph LR A[开始] --> B[初始化参数] B --> C[预测阶段] C --> D[计算卡尔曼增益] D --> E[更新估计值] E --> F[结束] ``` 在卡尔曼滤波的数学模型中,有以下关键步骤: - 预测方程:使用系统的状态转移矩阵来预测下一时刻的状态。 - 更新方程:使用卡尔曼增益来合并新接收到的测量值和预测值,以得到最优状态估计。 ### 2.2.2 帕斯瓦尔滤波器 帕斯瓦尔滤波器是一种专门用于频域的滤波器,它利用傅立叶变换将信号从时域转换到频域,在频域中进行滤波操作。帕斯瓦尔滤波器通常用于周期性噪声的消除。 ```mermaid graph LR A[开始] --> B[信号傅立叶变换] B --> C[设计滤波器频率响应] C --> D[应用滤波器] D --> E[逆傅立叶变换] E --> F[结束] ``` 帕斯瓦尔滤波器的主要步骤包括: - 将时域信号进行傅立叶变换以获取其频域表示。 - 根据需要过滤的频率设计滤波器的频率响应。 - 应用设计好的滤波器进行频率域的滤波操作。 - 进行逆傅立叶变换得到滤波后的时域信号。 ### 2.2.3 粒子滤波器 粒子滤波器是一种基于蒙特卡洛模拟的递推贝叶斯滤波算法,用于非线性和非高斯噪声环境下的状态估计。粒子滤波器通过一组随机样本(粒子)来代表概率分布,并通过重采样和权重更新来逼近真实状态的概率密度函数。 ```mermaid graph LR A[开始] --> B[初始化粒子] B --> C[预测新粒子位置] C --> D[计算新粒子权重] D --> E[进行重采样] E --> F[状态估计] F --> G[结束] ``` 粒子滤波的执行过程包括: - 初始化一组粒子,每个粒子代表一个可能的状态。 - 对每个粒子根据系统的动态模型预测下一时刻的状态。 - 根据新观测数据调整粒子的权重。 - 通过重采样步骤来避免权重退化问题,保持粒子多样性。 - 根据粒子的权重合成出最优的状态估计。 ## 2.3 滤波性能评估指标 ### 2.3.1 精度与稳定性分析 在评估滤波算法的性能时,首先需要关注的是算法的精度和稳定性。精度通常指的是滤波结果与真实值之间的误差大小。而稳定性分析则是检查滤波结果随时间变化的一致性和可靠性。 - 精度评估常用指标包括均方误差(MSE)和绝对误差。 - 稳定性评估通常通过长期监测滤波输出来完成。 ### 2.3.2 计算复杂度与实时性评估 滤波算法的计算复杂度决定了算法的运行速度,它在很大程度上影响了算法的实时性。对于需要实时处理IMU数据的应用来说,算法的计算效率至关重要。 - 计算复杂度主要通过算法的运算次数和内存需求来衡量。 - 实时性可以通过算法处理数据所需的时间和完成任务的频率来评估。 对于具体的算法选择和优化,需要在保证精度和稳定性的前提下,考虑到实际应用中对计算资源的限制和实时处理的需求。 # 3. IMU数据滤波算法实践 ## 3.1 环境噪声对IMU数据的影响 ### 3.1.1 环境噪声的来源和特性 在使用惯性测量单元(IMU)时,不可避免地会遇到环境噪声的影响。这些噪声可能来源于传感器内部的电子器件,也可能来自于传感器外部的环境因素。例如,温度变化可能会引起内部元件的热噪声;机械设备运行或电磁干扰可能导致外部噪声;还有因为地面振动或其他动态干扰